
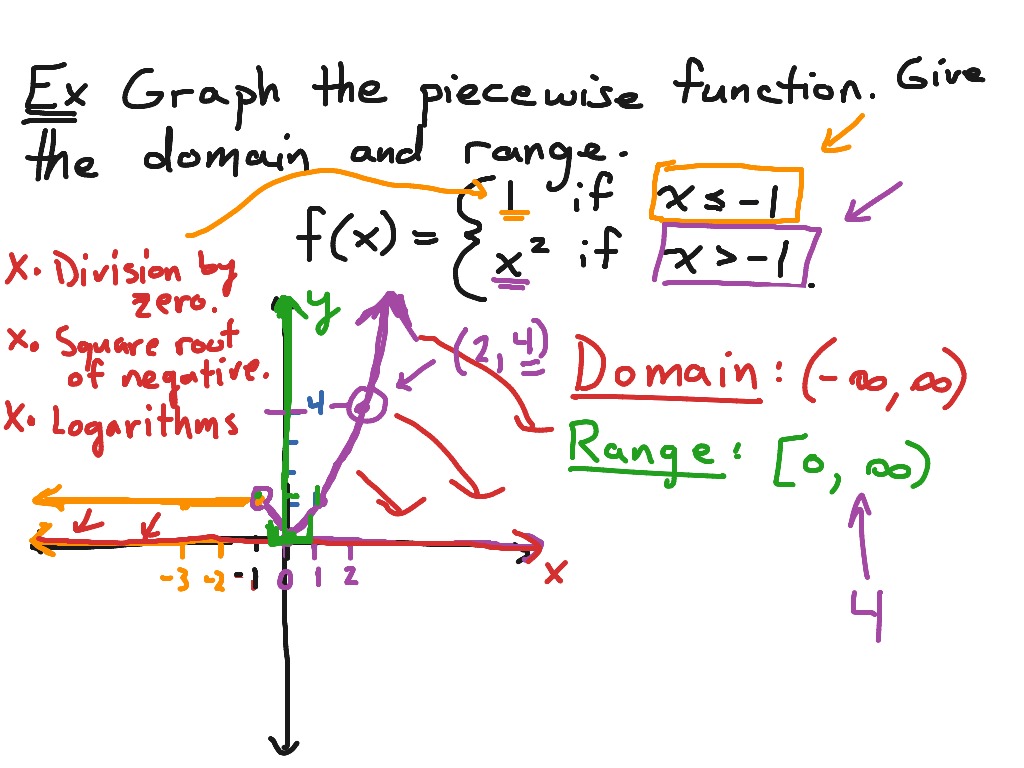
In interval notation, we use a square bracket. We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. We also need to consider what is mathematically permitted.
Domain and range of piecewise functions movie#
Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples, such as tickets sales and year in the horror movie example above. In this section, we will practice determining domains and ranges for specific functions. In Functions and Function Notation, we were introduced to the concepts of domain and range. Since x includes -3 and 3 we use to show the number between So -3 ≤ x ≤ 3, becomes If it was 4 < y ≤ 10, it would be (4, 10] ( ) shows that the end numbers are not included in the solution set.Figure 1 Based on data compiled by 3 Finding the Domain of a Function Defined by an Equation Find what makes an even root (square root, 4th roots and so on) inside negative.ġ4 Interval Notation Find the Implied Domain After setting 9 – x2 = 0 and finding the answer -3 ≤ x ≤ 3, easier said then done. Piecewise functions different functions over different parts of a domain Here is the Rule of the piecewise function (0,2) If x = - 2, then 2(-2) + 2 = -2 If x = 0, then -3(0) – 1 = -1 If x = 1, then -3(2) – 1 = -4 (0, - 1) (1, -4) (-2, -2)ġ2 Implied Domain, the real numbers in which the function is definedĭomain where x does not equal 5 or All real numbers except 5 All real numbers except Where x greater then or equal to 0įind what makes the denominator of a fraction zero. X2+ y= 8 Solve for y= - x2+8 Y has only one answer so it is ok x2+y2=25 Solve for Not a functionĨ Function notation Use f(x) to stand in for y in the equation y = 5x – 2, so it becomes f(x) = 5x – 2 Why would we need this notation?
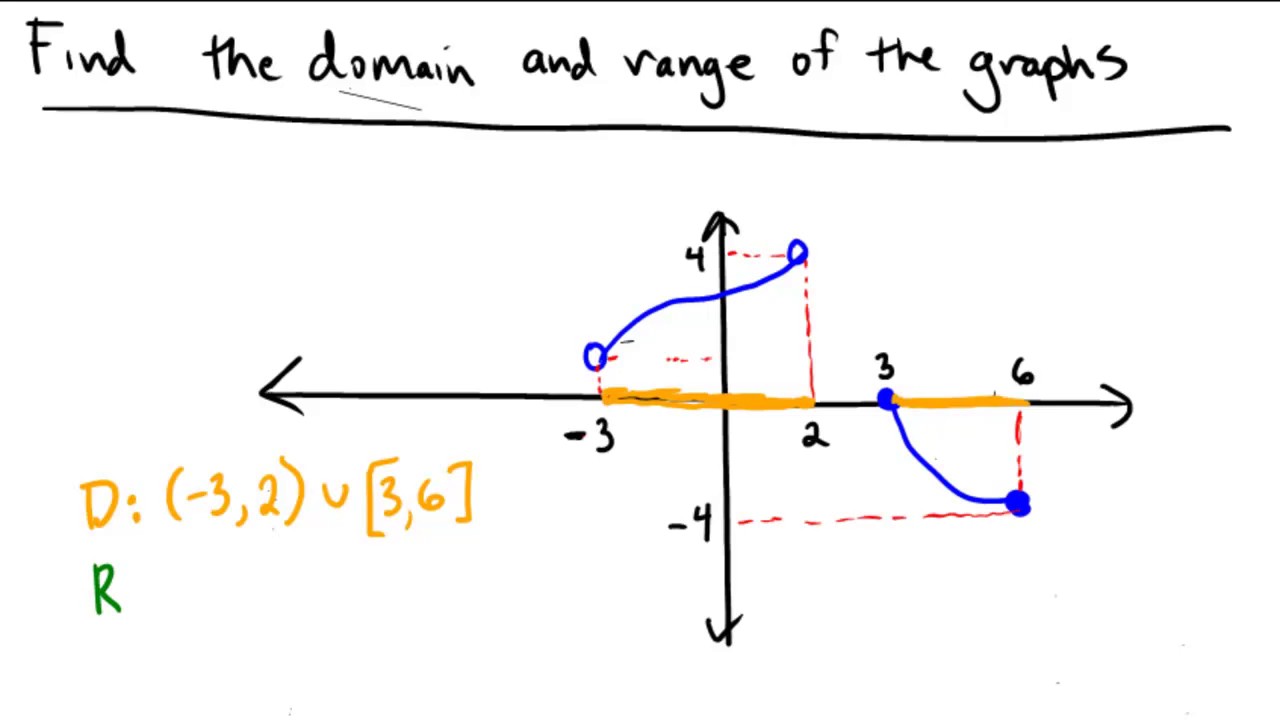
Algebraically is where you solve an element of the range. If a vertical line touches the graph in more then one spot, then the graph is not the graph of a function.

For example (1, 5), (2, 3) and (2,1).ħ Testing a function Graphically uses the vertical line test. If an element from the Domain has two different outcomes, it is not a function. Verbally How the input effect the output Numerically A table of numbers Graphically With a graph Algebraically With an equationĦ Testing a Function Verbally with a Proof Numerically with a table. Every time.Ĥ Elements in the Domain only map to one element in the RangeĪ x An element in the b y Range can have c z many Inputs, Where d w the Domain can only go to one element in the Range. Relations are functions, functions match elements from the domain to the rangeģ A Function A car’s brake pedal is part of a function car. Range is the Output (Dependent variable) given by the function. 1 1.3 Functions Domain and Range Function notation Piecewise functionsĢ Domain and Range Domain is the Input (Independent variable) used in a function.


 0 kommentar(er)
0 kommentar(er)
